The common belief is that a tossed coin has a 50% chance of landing heads up and a 50% chance of landing tails up. Sounds logical: the coin is symmetrical, each side is equal, and the chance of falling on one of them is 50/50.
That’s a foundational concept in probability theory and is often used in decision-making, games, and sports to ensure fairness. It’s simple, it’s clean, and it’s easy to understand.
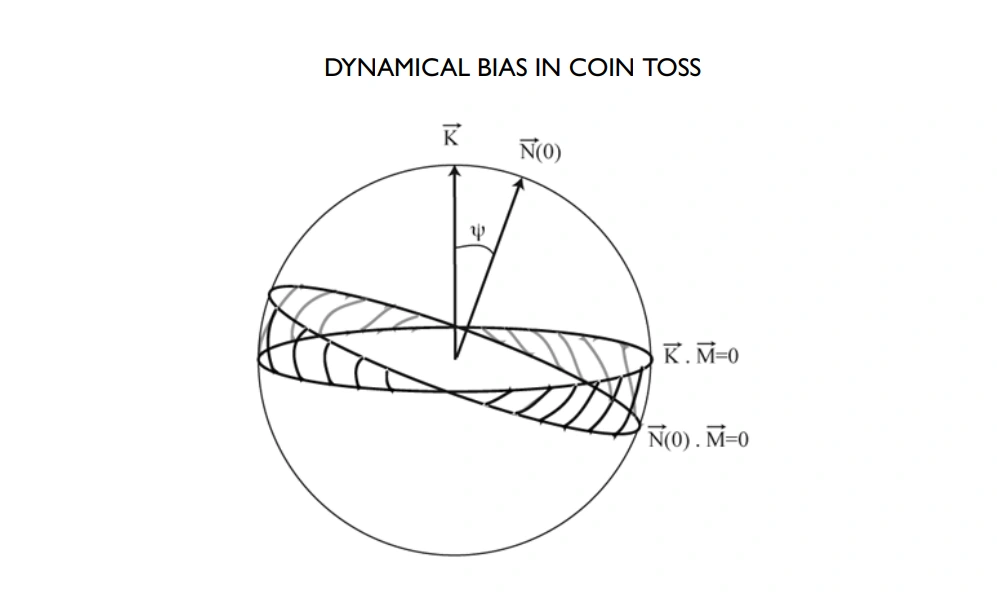
The Diaconis-Holmes-Montgomery theory on coin flipping dives deep into the actual dynamics of the act. Contrary to the popular belief of a 50/50 outcome, they found that a coin is slightly biased to land on the side it started on. So, if you start with heads facing up and give it a good toss, there’s a tad more than a 50% chance it’ll land heads up again.
So, does it mean the coin flip isn’t 50/50?
While most of us grew up thinking that flipping a coin is the gold standard of fairness, Diaconis and the team delved into the physics of the action. So the real distribution is closer to 51%/49%, with a little bias to the side you started to flip with.
And as with any other thing performed by a person, you have a chance to manipulate results if you learn how to toss a coin the right way. So you can maximize the chance it will lend the right way.
But think about this:
- Real-World vs Controlled Environment: Okay, their findings matter. But they were derived under controlled conditions. In the real world, there are too many factors, like find, surface, the power of flip, and human inconsistency. All of this impacts the results in the real world. So, can we truly generalize their findings to every coin flip at a soccer match or between friends at a diner?
- Significance of the 1%: The theory says there’s a 1% bias. But is this 1% significant? In most cases, that’s just an observational error. Such an error decreases when we conduct more coin flips. That means when we can get any results if we flip a coin, for example, 10 times, the more flips we conduct, the more results would be headed to 50-50 distribution. That slight bias might not make a real-world difference for most decisions made on a coin flip.
- Replicability of the Experiment: Critical thinking demands we question if other researchers, under different conditions, can replicate the same results. Have there been enough independent verifications of the Diaconis findings to stamp it as an undeniable truth?
- Complexity for Simplicity’s Sake: The coin flip’s beauty lies in its simplicity. Introducing physics and starting positions might make the process more complex than it needs to be. Is there a risk of overcomplicating a tool that’s meant to simplify decision-making?
- The Human Factor: The theory heavily leans on physics, but what about the human element? Can individuals consistently flip a coin with the same force and trajectory each time? Probably not. Human variability could easily overshadow the slight bias the theory proposes.
- Intentionality: For the bias to truly matter, a person would need to be aware of it and intentionally use it to their advantage. How many people flipping coins are doing so with the knowledge and precision required to exploit this bias?
One coin flip vs. statistical distribution
Statistics don’t say that a coin flip has a 50-to-50 chance of landing on one of the sides. We shouldn’t confuse the chance of the outcome for one coin flip and the statistical distribution of such coin flips. When we say the chances are 50/50, when we speak from the mathematical and statistical point of view, it is something that depends on the sample size: the bigger the sample, the more accurate the distribution. For example, I can get almost any result when I flip a coin 10 times.
I tried it myself, and for 30 flips, I got such results:
1st attempt (10 tosses):
- Heads: 7 times
- Tails: 3 times
2nd attempt (10 tosses):
- Heads: 6 times
- Tails: 4 times
3rd attempt (10 tosses):
- Heads: 6 times
- Tails: 4 times
For 30 tosses, that’s:
- Heads: 19 times
- Tails: 11 times
Looks like not a 50-50 distribution. But if I keep flipping a coin, the results would be closer to 50-50. In math, it’s called tending to 50-on-50. The more I flip a coin, the more the results will approach a perfect distribution because that depends on the sample size. If I were flipping a coin infinite times, I would get a distribution of 50-to-50.
So yes, flipping a coin isn’t always 50/50, as another factor can impact it: how you flip, wind, and other things. But there’s a solution. For example, you can toss a coin online, like here. There’s no physics involved, so the results are determined purely by probability, and the chances are really 50/50. But once again, these chances work with large numbers, representing the law of large numbers. We need to have a huge sample size to get a distribution closer to 50-to-50 probability. And even if there’s a 1% bias, from a statistical point of view, it’s not important and can be so due to different factors.
Of course, you can learn how to toss a coin to increase chances for the right outcome, but when we speak in general, like tossing a coin with your friend,






